1 Anwendung in der Betriebsprüfung
1.1 Der Chi-Quadrat-Anpassungstest für Tagesumsätze
Bei bargeldintensiven Betrieben interessieren sich Betriebsprüfer für die Bareinnahmen. Nicht die tatsächlichen Einnahmen, sondern einen geringeren Betrag anzugeben, scheint verlockend zu sein, um gleich mehrere Steuerarten zu hinterziehen.
Die „Forschungshypothese“ des Betriebsprüfers ist gemäß seinem Auftrag am besten mit „ich vermute, dass der zu prüfende Betrieb Zahlen manipuliert hat“ zu beschreiben. Bei den täglichen Bareinnahmen konkretisiert sich dies zu „ich vermute, dass der zu prüfende Betrieb nicht die tatsächlich angefallenen Bareinnahmen angegeben hat.“ Da es in der Regel für den Betrieb wirtschaftlich keinen Sinn machen dürfte, zu hohe Bareinnahmen anzugeben, wird hieraus „ich vermute, dass der zu prüfende Betrieb zu geringe Bareinnahmen angegeben hat.“
Nun wird recht willkürlich unterstellt (mehr dazu hier), dass die wirklichen Tageseinnahmen einer Lognormalverteilung folgen. Es ist nicht leicht, Umsätze zu manipulieren und gleichzeitig die Form der Verteilung einzuhalten. Daher biete es sich an, zu prüfen, wie gut die Verteilung der Tagesumsätze sich an eine Lognormalverteilung anpassen lässt. Wenn sie sich schlecht daran anpasst, so läge die Vermutung nahe, dass Zahlen manipuliert wurden.
1.2 Praxisbeispiel
1.2.1 Betrieb
Es handelt sich um einen bargeldintensiven Betrieb.
1.2.2 Daten
Es liegen aus den Jahren 2011, 2012 und 2013 insgesamt 914 Beobachtungen vor. Diese teilen sich wie folgt auf:
| Tag \(d\) | \(N_d\) — Anzahl Beobachtungen | Durchschnittlich- er Umsatz \(\bar{x}_d\) | Standardab- weichung \(s_d\) |
| Montag | 148 | 139.90 | 61.89 |
| Dienstag | 155 | 193.42 | 83.80 |
| Mittwoch | 152 | 166.87 | 68.59 |
| Donnerstag | 152 | 177.02 | 70.71 |
| Freitag | 153 | 245.93 | 87.04 |
| Samstag | 154 | 168.31 | 68.28 |
1.2.3 Schichtung
Schichtung ist auch als Gruppierung, Klassifizierung, Pooling bekannt. Es geht darum, Beobachtungen in geeigneten Gruppen zusammenzufassen, und diese dann gruppenweise zu analysieren. Hier
„wurde festgestellt, dass die Wochentage Montag bis Donnerstag in einem nahezu identischen Einnahmebereich liegen. Lediglich der Freitag weist deutlich erhöhte und der Samstag leicht erhöhte Tageseinnahmen im Vergleich zu dem Rest der Woche auf. Die Verteilungsanalyse wurde daher getrennt für die beiden Erlösebenen durchgeführt.“
Dem aufmerksamen Leser fallen in dem ersten Satz bereits drei Erlösebenen ins Auge, nämlich
- Montag–Donnerstag
- Samstag (leicht erhöht)
- Freitag (deutlich erhöht).
Vom Prüfer gemeint sind die beiden Erlösebenen Montag–Donnerstag und Freitag+Samstag. Wie nun „deutlich erhöht“ und „leicht erhöht“ definiert sind, warum zwei offensichtlich unterschiedliche Verteilungen (Freitag und Samstag) gepoolt werden und nach welchen Kriterien genau sich damit die Schichtung ergibt, bleibt unerklärt.
Betrachtet man die Mittelwerte und Standardabweichungen der Umsätze der einzelnen Tage in der obigen Tabelle, so kommen auch ohne vertiefte Statistikkenntnisse erhebliche Zweifel bezüglich der Vergleichbarkeit der Tagesumsätze auf. Das Vorgehens des Prüfers erscheint somit zumindest fragwürdig und bedarf einer guten Begründung. Auch fragt man sich: Wenn der Samstag mit einem Mittelwert von EUR 168 „leicht erhöhte Tageseinnahmen“ aufweist, wieso fällt der Dienstag mit durchschnittlich EUR 193 dann in eine Kategorie mit dem Montag, der lediglich EUR 139 im Durchschnitt aufweist?
1.2.4 Analyse des Prüfers
Für die Montags- bis Donnerstagsumsätze ergibt sich bei Vergleich mit einer Lognormalverteilung mit Lagemaß 2.207 und Streuungsmaß 0.210 (Logarithmen wurden etwas unüblich zur Basis 10 berechnet) eine Teststatistik von 28.36, die links vom kritischen Wert \(\chi^2(0.9995,df=13)=36.48\) liegt, berechnet.
Für die Freitags- und Samstagsumsätze ergibt sich bei Vergleich mit einer Lognormalverteilung mit Lagemaß 2.347 und Streuungsmaß 0.266 (Logarithmen wurden etwas unüblich zur Basis 10 berechnet) eine Teststatistik von 51.67, die rechts vom kritischen Wert \(\chi^2(0.9995,df=11)=33.14\) liegt, berechnet.
Welches Signifikanzniveau nun tatsächlich angewendet wird, ist aus dem Schreiben nicht ersichtlich. Es werden die Werte 1% und 0.05% genannt, aber eine Festlegung erfolgt nicht. Die p-Werte betragen 0.0081 (Mo-Do) und 3.128e-7, zu den meisten gängigen Signifikanzniveaus würde die Nullhypothese also verworfen werden.
1.2.5 Ergebnis
Die Forschungshypothese wird so bestätigt und das Prüfungsziel wird erreicht:
„Um die aus den o.g. Mängeln resultierende Unsicherheit auszugleichen wird im Rahmen der Betriebsprüfung ein Unsicherheitszuschlag i.H.v. 7% der Umsätze festgesetzt. Die netto Unsicherheitszuschläge des Prüfungszeitraums betragen: …“
Wieso es nun genau \(7\%\) sein sollen, ist mir unklar. Es ließe sich aus der Abweichung von der Verteilung durchaus der Effekt durch Truncation oder Censoring abschätzen.
2 Fallstricke
Der Prüfer statuiert in seinem Schreiben, dass
„die grafischen Auswertungen und die mathematisch ermittelten Gegenwahrscheinlichkeiten auf eine Erlöskappung der hohen Tageseinnahmen“
hindeuteten. Einer genaueren Betrachtung hält die statistische Analyse jedoch nicht stand. Er hat hier — recht offensichtliche — Fallstricke ignoriert, die wir uns ansehen wollen.
2.1 Ungeeignete "Schichtung"
2.1.1 Einfaches Beispiel (Simulation)
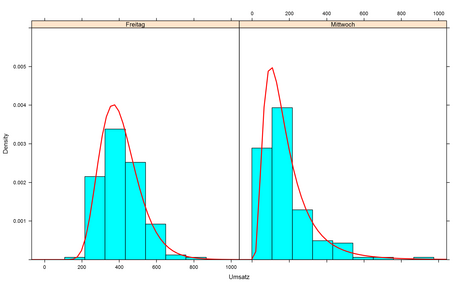
Um das Problem zu illustrieren, nehmen wir ein Beispiel her: Ein Betrieb erwirtschaftet tatsächlich lognormalverteilte Tagesumsätze. Am Mittwoch sind es im Median \(\sim 150\) Euro, und am Freitag sind es im Median \(\sim 400\) EUR. Wir simulieren die Werte von 150 Mittwochen und Freitagen. Die blauen Kästen enthalten Copy&Paste–fähigen R–Code, falls der Leser die Simulation selbst durchführen möchte.
t.df <- data.frame(
Umsatz=c(
rlnorm(150,meanlog=5,sdlog=0.6),
rlnorm(150,meanlog=6,sdlog=0.25)
),
Tag=rep(
c('Mittwoch',
'Freitag'),
each=150
)
)
Stellen wir uns diese Daten jetzt dar, so zeigen sich erhebliche Unterschiede zwischen den Tagen, aber jeder Tag passt erstaunlich gut zu einer Lognormalverteilung, deren Dichte in der Abbildung unten als rote Kurve eingezeichnet wird.
library(lattice)
dev.new(width=12.95, height=8)
histogram(~Umsatz|Tag,
data=t.df,
type='density',
ylim=c(0,0.006),
panel = function(x, ...) {
panel.histogram(x, ...)
panel.mathdensity(dmath = dlnorm,
col = "red",
lwd=2,
args = list(
meanlog=mean(log(x)),
sdlog=sd(log(x))
)
)
}
)
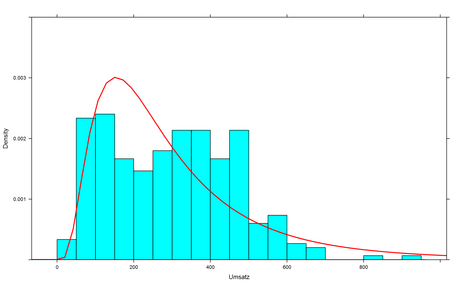
Kommen wir nun auf den Gedanken, diese Daten in einen Topf zu werfen, so ergibt sich folgendes Bild. Die rote Kurve ist die am besten dazu passende Lognormalverteilung, und wir stellen fest, dass diese nicht sonderlich gut passt. Um den Umsatzwert 200 herum übersteigt die rote Kurve die empirisch ermittelten Werte erheblich. Rechts davon (Umsätze von EUR 300 und mehr) liegt die Kurve erheblich unter den beobachteten Werten. Ganz am rechten Rand fehlen zu der Kurve passende beobachtete Werte fast vollständig.
dev.new(width=12.95, height=8)
histogram(~Umsatz,
data=t.df,
type='density',
ylim=c(0,0.004),
breaks=20,
panel = function(x, ...) {
panel.histogram(x, ...)
panel.mathdensity(dmath = dlnorm,
col = "red",
lwd=2,
args = list(
meanlog=mean(log(x)),
sdlog=sd(log(x))
)
)
}
)
Dies liegt aber nicht daran, dass Zahlen manipuliert wurden. Wir wissen von oben, dass die Daten wirklich aus Lognormalverteilungen stammen. Die gepoolten Daten aber stammen nun nicht mehr aus einer Lognormalverteilung, sondern aus einer Mischungsverteilung, die aus zwei Lognormalverteilungen besteht. Vergleicht man die gepoolten Daten mit einem \(\chi^2\)–Anpassungstest mit einer Lognormalverteilung, so wird dieser die Nullhypothese, dass die Daten lognormalverteilt sind (fast) immer ablehnen. Die falsche/unterlassene Schichtung der Daten erzwingt so ein für den geprüften Betrieb unvorteilhaftes Testergebnis, obwohl alle Daten aus Lognormalverteilungen stammen.